Talk:Evoptool: Evolutionary Optimization Tool
Contents
New Page
Evoptool Description
Algorithms
Evoptool offers a set of algorithm implementations coming from several paradigms within Evolutionary Computation, in the context of black-box optimization of boolean functions.
- Genetic Algorithms (GAs)
- Simple Genetic Algorithm (SGA). It is the original genetic algorithm with truncation selection, bitflip mutation, and single-point crossover.
- SGA with binary tournament selection. It is a variation of the SGA, and it differs for the selection operator that implements a binary tournament selection. Two individuals are picked up randomly from the population, and their fitness compared: the fittest individual is selected for the new population.
- SGA with uniform bitwise crossover. Another variation of SGA, it maintains the truncation selection and bitflip mutation, but implements a uniform bitwise crossover. This variation operator looks each bit of the two individuals string and swap them with a fixed crossover probability.
- Estimation of Distributions Algorithms (EDAs)
- Univariate EDAs:
- Population Based Incremental Learning (PBIL). It maintains a vector of marginal probabilities which is used to sample a new population at each generation. Then, after a selection of the population is performed, the marginal probabilities are computed again and the vector is updated according to a learning rule.
- Univariate Marginal Distribution Algorithm (UMDA). It differs from PBIL in having no learning rule. It simply generate new individuals using marginal probabilities computed as marginal frequencies of the previous population.
- Compact Genetic Algorithm (cGA). It is a space-efficient variation of PBIL that maintains a probability vector, but rather than generating a whole population, only two individuals are generated, from it and then are subjected to tournament. The probability vector is then updated according to a learning rule which considers both individuals.
- Univariate Distribution of Estimation Using Markov Random Field (Univariate DEUM). It uses an univariate Markov Random Field (MRF) to model the relationship between individuals and their fitness. MRF parameters are estimated through maximum likelihood, then the model is used to sample a new population by employing a Gibbs or Metropolis sampler.
- Bivariate EDAs:
- Mutual Information Maximizing Input Clustering (MIMIC). It adopts a directed conditional chain model for the distribution structure, learned by a greedy heuristic employing Shannon's Information Entropy, in order to minimize the Kullback-Leibler Divergence between the model and the true distribution.
- Combining Optimizers with Mutual Information Trees (COMIT). It is similar to MIMIC, but with a tree-structured Bayesian network rather than a single chain. A maximum weight spanning tree is used to learn the structure, guided by the entropy information principle. Once the structure is defined, it samples the individuals according to defined model, and then it exploits fast search algorithms to further improve the generated individuals. Inside Evoptool there are two implementation: one with an hill-climber fast search, and one with a PBIL based fast search.
- Bivariate Chain DEUM (Bivariate DEUM). It differs from the univariate version only for the structure of the underlying probabilistic model, that takes the form of a bivariate undirected chain.
- Ising Model DEUM (Ising DEUM). It is a DEUM like algorithm specifically designed to solve the Ising Spin Glass problem, by employing a bivariate lattice structure.
- Multivariate EDAs:
- Simple Bayesian Optimization Algorithm (sBOA). It uses a Bayesian network to represent the fitness structure, it employs the Bayesian-Dirichlet metric to measure the network quality, and a greedy algorithm to search the space of possible networks. At each generation, it computes and stores in the network the marginal and conditional probabilities of a selection of the original individuals, and than uses the Bayesian network to generate the new population.
- Univariate EDAs:
Benchmarks
Evoptool is designed to support the study of black-box optimization for boolean functions. The fitness function of each benchmark accepts as argument a string of boolean variables and returns a real value. Being performance comparison the main purpose of Evoptool, it already includes several optimization problems with different properties, varying from classical toy problems to more complex ones.
A first set of benchmarks is composed of simple toy problems without any variable dependency, therefore with an underlying univariate structure.
- One Max. A simple problem where the returned value is represented by the count of alleles of the individual taking value one. It has a unique optimal solution and every allele has the same relevance in the individual.
- One-Zero Max. It is a variation of One Max, where the fitness of an individual is represented by the maximum between the count of zeros and the count of ones. The relevant property of this problem is the existence of two optimal solutions: one with all alleles taking value one, and one with all zeros.
- Sum Value. In this toy problem the optimal solution is represented by a string of all ones. The fitness value is computed as the sum of the products between alleles and coefficients equal to the allele position inside the string. Also in this case there are no variable dependencies, but in contrast to the previous benchmarks the relevance of each allele is different and it grows linearly.
- Binary Value. Very similar to the Sum Value benchmark, it gives an increasing quadratic relevance at each alleles.
Another group of functions is constituted by deceptive problems, designed to mislead classical Genetic Algorithms. Their structure defines dependencies among variables with different orders (bivariate, trivariate, multivariate).
- Alternated Bits. Also called 1D Checkerboard, it introduces dependencies between couples of adjacent variables defining a chain structure. The problem takes into account the value of a variable relative to that of its immediate neighbours in the chain, in particular, higher fitness is achieved when neighbourring variables take opposite values.
- F3-Deceptive, Overlapping and Bipolar. This deceptive function is composed of separable building blocks of order three which has one global optimum for all ones and a deceptive local optimum to all zeros. The final fitness value is composed by the sum of the contributions of each deceptive pattern defined on three consecutive bits. The Bipolar variant is based on blocks of six bits, where there are two global optimum (all ones and all zeros) and a deceptive local optimum(three ones and three zeros). Overlapping version introduces overlaps among building blocks.
- Trap-5. This benchmark is similar to previous deceptive functions, and differs for the length of building blocks. As the previous functions, it has a global optimum for all alleles taking value one, and a deceptive local optimum for all zeros.
- Four Peaks and Six Peaks.
Last but not least, there are implementation of real-like applications as:
Statistics
Compile the Source
Entire Tool
Individual Library
Run the Tool
GUI
Command Line
Source Documentation
Download Evoptool
Old Page
User Manual
Compile and Run Evoptool
Compile all the project
- In the main folder ../evoptool/trunk/ give a make cleanall command in order to remove all the binary files and library dependencies, and be sure to compile the entire project in the right way.
- In the main folder ../evoptool/trunk/ give a make all command in order to compile all the libraries and build the executable file.
Compile only some libraries
- In the folder ../evoptool/trunk/mylib/src/ give a make lib command in order to compile and build library associated with that module. Repeat this operation for each library you want to compile.
- In the folder ../evoptool/trunk/gui/src give a make exe command in order to build the executable file.
Run the tool
- Go to the ../evoptool/trunk/gui/bin/ folder.
- Run the software with the ./evoptool command.
Algorthms
This section have the purpose to show the set of algorithms implemented inside evoptool. These algorithms belong to different classes, and they perfom different operations. In the following lines are presented the theoretical bases for better undestand the use of evoptool.
- Genetic Algorithm (GA). Is a search technique used in computing to find exact or approximate solutions to optimization and search problems. They grow a population of abstract representations (chromosomes or genotype) of candidate solutions (individuals or phenotypes) to an optimization problem evolves toward better solutions. In this tool, solutions are represented as binary strings of 0s and 1s, but other encodings are also possible. The evolution usually starts from a population of randomly generated individuals and happens in several generations (selection, crossover, mutation). The new population is then used in the next iteration of the algorithm. Commonly, the algorithm terminates when either a maximum number of generations has been produced, or a satisfactory fitness level has been reached for the population. Nowaday, there are the following GA implemented inside evoptool:
- SGA (Simple Genetic Algorithm). A selection operator is applied to the population and two random recombinator operators called crossover and mutation are applied to the selected population in order to improve the population. SGA uses a truncation selection with a fixed percentage. The variation operators used are Uniform crossover and Bit-Flip mutation.
- SGA with Binary Tournment.
- SGA with Population Wise Uniform Crossover.
- SGA (Simple Genetic Algorithm). A selection operator is applied to the population and two random recombinator operators called crossover and mutation are applied to the selected population in order to improve the population. SGA uses a truncation selection with a fixed percentage. The variation operators used are Uniform crossover and Bit-Flip mutation.
- Estimation Distribution Algorithm (EDA). Is powerful population-based searcher where the variation operations traditionally implemented via crossover and mutation in EAs are replaced by the process of random sampling from a probability distribution. The distribution is modified generation after generation, using information obtained from the fitter individuals in the population (estimation). The objective of these changes in the distribution is to increase the probability of generating individuals with high fitness. In our tool there are several EDA implemented such:
- cGA (Compact Genetic Algorithm). It initialize a vector of probabilities where each component follows a Bernoulli distribution with parameter 0.5. Next, two individuals are generated randomly from this vector of probabilities. After the individuals are evaluated, a competion between then is carried out. The competion is held at level of each of the unidimensional variables, in such a way that if for the ith position the conquiring individual take a value different from the loser, the ith component of the vector of probabilities increases its value.
- PBIL (Population Based Incremental Learning). It maintains unconditional probabilities and no interparameter dependencies are modeled. A vector, P, specifies the probability of generating a 1 in each bit position. Initially, all values in P are set to 0.5. A number of solution vectors are generated by stochastically sampling P; each bitis sampled independently of all the others. The probability vector is then moved towards the generated solution vector with the highest evaluation.
- UMDA (Univariate Marginal Distribution Algorithm). At each generation, it estimate the joint probability distribution model of the selected individual by factorize it as product of indipendent univariate marginal distributions. Each univariate marginal distribution is estimated from marginal frequency.
- MIMIC (Mutual Information Maximizing Input Clustering). It attempts to communicate information about the cost function obtained from one iteration of the search to later iterations of the search directly. There are two main components of MIMIC: first, a randomized optimization algorithm that samples from those regions of the input space most likely to contain the maximum; second, an effective density estimator that can be used to capture a wide variety of structure on the input space, and that build a Markov Chain in order to represents the bivariate structure.
- COMIT (Combining Optimizers with Mutual Information Trees). It gains most of the benefits of modeling the dependencies in the search space at a significantly reduced computational cost. COMIT starts by estimating a probabilistic model of the population, than uses the model to stochastically generate new solutions, it selects the fittest solutions and perfom a local fast-search initialized with these solutions.
- COMIT with HillClimbing as fast-search.
- COMIT with PBIL as fast-search.
- DEUM (Distribution Estimation Using Markov Random Field). DEUM uses MRF approach to estimate and sample the probability distribution using a fitness modelling approach to estimate the MRF parameters. This version of DEUM is an univariate model of probability distribution. This allows to completely eliminate the structure learning task.
- DEUM with probability vector. It uses the estimated parameters of MRF for update the probability vector, generation by generation.
- DEUM with direct sampling from Gibbs distribution. It uses the estimated parameters of MFR for directly calcutate the probability of each bit to be 1 or 0.
- Is-DEUM (Ising model DEUM). It is an evolution from the univariate DEUM to a bivariate version. This algorithm has been defined for solve the Ising Sping Glass problem, and therefore it use a grid structure to model the interactions between each variables of a solution.
- Is-DEUM with a Metropolis sampler.
- Is-DEUM with a Gibbs sampler.
- sBOA (Simple Bayesian Optimization Algorithm). It is a multivariate EDA that uses the Bayesian Dirichlet equivalence metric to measure the goodness of each structure. The search used is a greedy search and it starts in each generation from scratch. In order to reduce the cardinality of the search space the constraint that each node in the Bayesian network as at most k parents is assumed.
- Genetic Estimation Distribution Algorithm (GEDA). This class of Evolute Algorithms is a new proposal class, where genetic variation operations such mutation and crossover are applied to a probabilistic model of the population, rather than directly to an individual of the population. Each generation of a GEDA is composed by estimation of population distribution, variation of the probabilistic model, and sampling from the variated model.
- gcGA.
- Operative Reaserch classical algorithms (OR). It is distinguished by its frequent use to examine an entire management information system, rather than concentrating only on specific elements. An operations researcher faced with a new problem is expected to determine which techniques are most appropriate given the nature of the system, the goals for improvement, and constraints on time and computing power. For this and other reasons, the human element of OR is vital. Like any other tools, OR techniques cannot solve problems by themselves.
- Pseudo Boolean Linear Programming.
Optimization Problems
An optimization problem is defined by a specified problem space X, an objective functions F , a search space G, a set of search operations A. Specifying the elements of this tuple is the most important prerequisite for any experiment. The problem space X is the space of all possible solutions canditates, in our case is defined by every combinations of a fixed lengh bit string. The objective functions F (fitness) measure the utility of a solution. As convention, we decide that every objective function return a real number between in the [0,100] set, and if nothing else is stated, maximization is assumed. The search space G is the space of elements where the search operations are applied. For evoptool is defined by the individual lenght (size). The search operations A are all the operations used for perform the search, and such we compare several algorthms a time, they are defined by the particular algorthm used.
Inside evoptool, is possible to choose between several different Objective Functions and customize a proper Optimization Problem setting the individual size and choosing a set of Algorithms to compare. The following list contains the Objective Functions implemented for the moment.
- AltBits.
- One Max and One Zero Max. The task in the OneMax problem is to find a binary string of length n consisting of all ones. The search and problem space are both the fixed-length bit strings G = X = Bn. Each gene (bit) has two alleles 0 and 1 which also contribute exactly this value to the total fitness.
- BinVal. It is something like a perverted version of the OneMax problem, with the objective function defined as the real value of the binary string. Since the bit at index i has a higher contribution to the fitness than all other bit at higher indices together, the comparison between two solution candidates x1 and x2 is won by the
lexicographically bigger one. We can expect that the bits with high contribution (high salience) will converge quickly whereas the other genes with lower salience are only pressured by selection when all others have already been fully converged.
- F3d Deceptive.
- F3d Deceptive Bipolar.
- F3d Deceptive Ovelapping.
- Four and Six Peaks. This Objective Function have some global optima wich are isolated, and therefore are difficult to find. It also have some local optima which are easy to get and therefore the search algorithms tend to converge on local optima.
- Trap5. Subjected to maximization based on the Hamming distance to a pre-defined global optimum X' . They build a second, local optimum in form of a hill with a gradient pointing away from the global optimum. This trap is specified with two values, b and r, where b corresponds to the width of the attractive basins (in our case b = 5)and r to their relative importance.
- Quadratic.
- Sat Lib.
- SumVal.
- Royal Road.
- Liepins Vose Fully Deceptive.
- SpinGlass. A spin-glass instance in the Ising model is given by n spins that can either point up or down. We consider two dimensional Edwards Anderson (EA) spin glass with +/-1 distribution and periodic boundary conditions. Spins are coupled with coupling strengh J. In an EA spin glass spins are located on the sites of a 2-dimensional lattice with nearest neighbor interactions being present. A set of problem instance for each problem size is provided with its best solution from The Spin Glass Ground State Server at the Institut für Informatik of the Universität zu Köln.
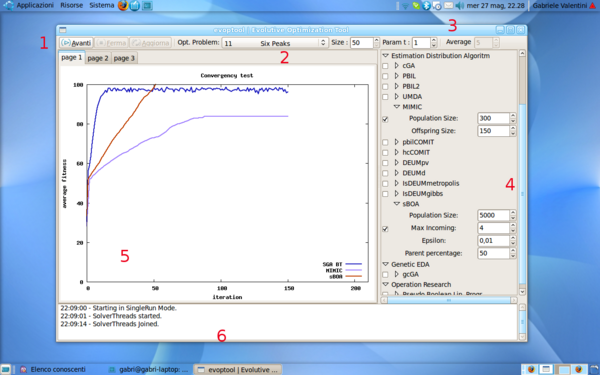
Graphic User Interface
The graphic user interface of evoptool is quite intuitive. The user can easily customize his own experiment, and visualize the results graph. In the next rows there are shortly described the GUI componets and their use.
- Control Buttons. There are three control buttons which can be used to start or stop the execution of an experitment, and to force the update of the graphs.
- Objective Function Settings. This part of the toolbar allows the customization of the Objective Problem. It is possible to select an objective function type and fix the individual size as number of bits.
- Average Mode Setting. Pushing this toggled button it is possible to enable Average Test Mode. In this mode, evoptool will run a difined number of algortihms for each selected one in the Algorithm Panel, and it will perform the average of the different executions of the same algorithm. This option is usefull to show the average behavior of searchers.
- Algorithms Panel. This panel allows to select a set of algorithms to compare in a particular execution. It is subdivided in four parts, in order to classify algorithms for belonging kind. Next, is possible to customize the parameters of each selected algorithm.
- Result Tabs. This tabs show the result graphics of the a test execution in real time mode. At this time, only the average fitness graph is implemented in evoptool, but new graphs can be easily added in future.
- Log Monitor. This monitor keep the user informed about the execution status and several others information such warnings or errors.
Video Example of Use
In this short video is briefly presented an example of use of evoptool. It starts by configuring the Optimization Problem to solve, next select a set of algortihms to compare and finally is showed the execution of a test.
Command Line
Evoptool is also powered by a command line interface, so when the GUI is not needed and can be an unusefull weight, it is possible to escape it and run the software just typing a command inside a terminal such bash or dash.
Commands
- --help (-h). This command print at video usefull information about evoptool commands and their use.
- --version (-v). This command print at video information about currently version of the software and others informations such Copyright or link to the evoptool web page.
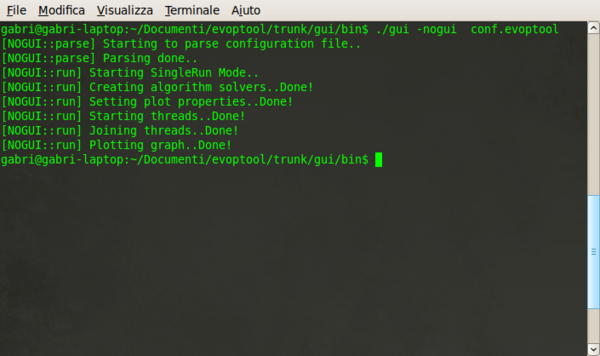
- --nogui [CONF_FILE] (-n). This is the more usefull command, such it allows to run evoptool from command line and to achieve the results as an image graph or, for more complex purposes, as data files. This command need only of one parameter that specify the CONFIGURATION FILE for the execution. The configuration file parameter need to be specified with a proper PATH if, and only if, its position differs from the program executable folder. In the next image is possible to view the output generated from an execution of a test from command line.
Configuration File
In order to run evoptool from command line, is needed a proper configuration file that define all the contraints and settings for that particulat test execution. A default configuration file can be found in the folder ../evoptool/trunk/gui/bin/confi.evoptool, and the user is free to customize it or to create a different file in a different position and specify the entire PATH before run evoptool. The configuration file is quite intuitive, and the default file presents several usuful information about the contents and how to modify it. It is subdivided in three main section, each of them define the behavior of a particular component.
- General Settings. Allows to specify if the execution of a test have to be a normal one (Single Run Mode), or an average execution (Multi Run Mode). In the last case, the parameter N_ALGO define the number of execution of an algorithm on that perform the average.
- Objective Function.Allows to specify which is the Objective Function for this test execution and to define the needed parameters as the individual size or others.
- Algorithms. Allows to define a set of algorithms to run, and to specify their parameters individually.
Some usefull information on how to customize the configuration file are listed in the next rows:
- Comment or uncomment lines with a simbol '#' for customize the configuration.
- Mandatory sections are signaled with a simbol '*', other sections can be deleted.
- Uneeded parameters must be commented!
- Values must be between square braces.
- Order of parameters inside sections is mandatory!
- There must be the end of file delimiter at last line.
Documentation
Evoptool is a software with the purpose to compare the performance of several different algorithms from the Evolutive family and, for obvious reasons, with some algorithms from the classical Operation Research family. Evoptool is written in C++ for the GNU/Linux platform and it exploit the Gtk libraries (in this case gtkmm libraries) and GNUplot utility. Inside this tool there are several implemented algorithms and some wrapped ones from already existing applications.
Software Modules
Evoptool is made up of several different modules (or libraries). This architecture make easy to organize files and better understanding how the application work.
- common - It contains commons classes and ancestors for the algorithm modules and for the optimization function module.
- ga - It contains the implementation of several Genetic Algorithms.
- eda - It contains the implementation of several Estimation Distribution Algorithms.
- geda - It contains the implementation of several gEDAs.
- or - It contains the implementation of some algorithms from the classical Operation Research.
- opt-pbl - It contains the implementation of several objective functions (fitness), that represents different problem instances.
- gui - This module is the main one, it contains all the classes for manage GUI (algorithm decorators). From the other side it implements the multithread mechanism under the GUI, and last but not list it contains the wrapped applications and take care about wrapping.
- misc - It contains general utility classes such rondom seed geerator.
Hierarchies
This section have the purpose to show some structures internal to evoptool implementation. In particular there are presented the main hierarchies of this software, so, future developers will be facilitated during the development of new componets.
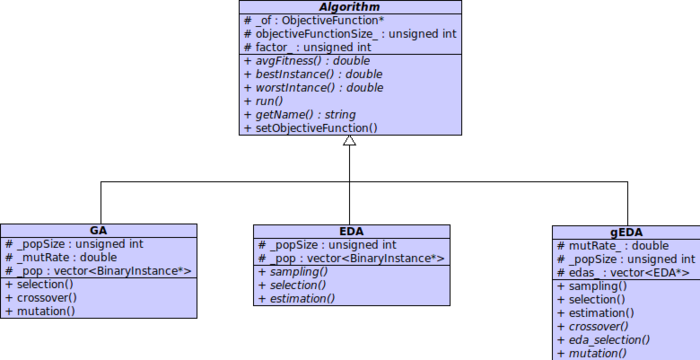
Algorithms Hierarchy
Every algorithm implemented inside evoptool inherits from the abstract class Algorithm. This defines every common attributes and functions, and it is an hight level of abstraction for an algorithm. Next, the others abstract classes GA, EDA, gEDA defines and some times implements common attributes and functions for each category of algorithm, in order to generalize more possible their own concepts. Finally every concrete algorithm will be inherits from one of those last abstract class, and will be a complete implementation of a particular kind of searcher.
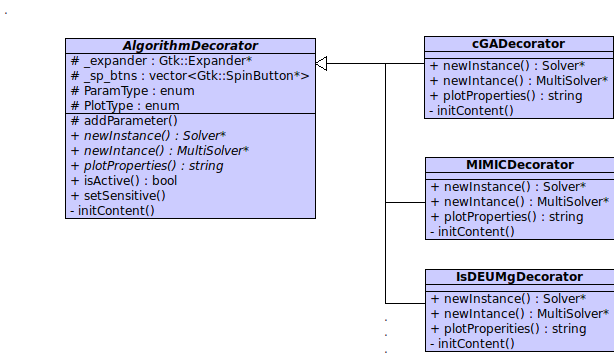
Decorators Hierarchy
Decorators are a very useufull and versatile objects. They allow to easily integrate a new algorithm in the graphic user interface. The abstract class AlgorithmDecorator define some functons that every concrete decorator have to implement. In addiction, it provides the function addParameter that allows a fast customization of each concrete decorator. Finally, a decorator can be viewed as a Wrapper for that algorithms that aren't directly implemented inside evoptool such sBOA.
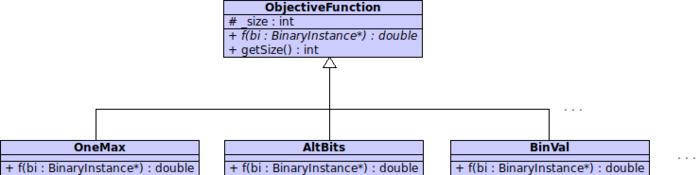
Objective Functions Hierarchy
This hierarchy define the structure of Objective Functions. As we can see, it is a quite simple architecture. Every objective functionions inherits from the abstract class ObjectiveFunction, that defines an abstract function f that represents the fitness function. Finally every concrete objective function have to implements this function as specified from the Optimization Problem.
How To Add New Features
Along the next sections will be presented some procedures to follow in order to add new features and components to evoptool. Those instructions are usefull to avoid common errors or to forget some parts of the implementation.
Add an Algorithm
Adding a new algorithm is really an easy task to do. The next lines will show the steps to follow in order to do it. As convenience, we will refere to a generic NewAlgorithm and it will be an algorithm of the category SomeGenetic.
- Create files. Create the files NewAlgorithm.h and NewAlgorithm.cpp inside the ../evoptool/trunk/somegenetic/src/ folder.
- Fill files. Every algorithm must inherits from the abstract class Algorithm, or from one of its abstract or concrete implementation. Such it have to be a concrete class, it must implments every abstract function inherited from its superclass.
- Create Decorator. See next section.
- Update Configuration Parser. See proper section.
Add a Decorator
In the following lines there are showed the steps to follow in order to add a new algorithm decorator to the grafic user interface. Here, we suppose to add a decorator called SomeAlgoDecorator for convenience, but obviously these instructions are valid for every decorator.
- Create files. Create the files SomeAlgoDecorator.h and SomeAlgoDecorator.cpp inside the ../evoptool/trunk/gui/src/ folder.
- Fill files. Every decorator must inherits from the abstract class AlgorithmDecorator, and must provides a concrete implementation of the abstract function:
- Solver* newInstance(...)
- MultiSolver* newInstance(...)
- string plotProperties(...)
- void initContent(...)
- Configure headers. Add the SomeAlgoDecorator.h to AlgorithmDecorators.h (note the 's'!) that is placed in the ../evoptool/trunk/gui/src/ folder. This will avoid to include a long list of decorator headers to the main GUI class.
- Add decorator to GUI. In order to concretly add the decorator to the GUI, is needed to modify the GUI.cpp class, adding proper code lines to the initAlgorithmDecorators function.
Update Configuration Parser
In order to add a new algorithm in the command line mode, it is need to modify and update the configuration parser, and to perfom other few task. As previous sections, we want to add a generic SomeAlgorithm to the Configuration Parser.
- Configure headers. Be sure that the file SomeAlgorithm.h is added to the header Algorithms.h (note the 's'!) that is placed in the ../evoptool/trunk/gui/src/ folder. This will avoid to include a long list of headers.
- Modify Configuration File. Add a new algorithm section to the end of the configuration file. Be sure to fix for that algorithm a proper free identification number. The section must contains every parameters needed by the algorithm.
- Update Configuration Parser. This task need to update the function parseAlgorithm of the file ConfParser.cpp placed in the ../evoptool/trunk/gui/src/ folder. Look that, such we can run evoptool in different run modes, there are two different implementation of this function that have a different return object. Remember to update both the implementation!
- Add a new case block to the switch/case structure. Be sure to use as case label the same number used before in the configuration file.
- Fill the case block with the code for parse the algorithm parameters. Parse every parameter using the just implemented functions. This will avoid to make errors and to spend a lot of time.
Add an Objective Function
This section will lists all the steps to follow in order to add a new objective function, and so add a new optimization problem, to evoptool. Here, we assume for convenience that the objective function to add is called SomeObjFun.
- Create files. Create the files SomeObjFun.h and SomeObjFun.cpp inside the ../evoptool/trunk/opt-pbl/src/ folder.
- Fill files. Every objective function must inherits from the abstract class ObjectiveFunction, or from one of its concrete implementation. It must implements or overwrites the abstract function f (fitness) inherited from its superclass.
- Configure headers. Add the SomeObjFun.h to ObjectiveFunctions.h (note the 's'!) that is placed in the ../evoptool/trunk/gui/src/ folder. This will avoid to include a long list of headers to the main GUI class.
- Update Enumeration. Add a new value for the enum GUI::ObjFunctions defined in the GUI header file. The header GUI.h can be found in the ../evoptool/trunk/gui/src/ folder.
- Update GUI. In order to link the just created fitness function with the grafic user interface it is needed to modify the GUI.cpp file.
- getSelectedObjectiveFunction function. Add the new component to the switch/case block.
- initObjList function. Add the new componet to the Gtk::TreeModel object, so it will be showed in the proper selection menu.
- Update Configuration Parser. This is a quite simple task to do, just look to the code!
Usefull Links
- Evoptool Repository (Need authentication!)
- GNU Scientific Library
- GUI Library Gtkmm
- Boost Library
- Gnuplot Utility
- C++ Library reference
ToDo List (only for developers)
- TOSO: UMDA check algorithm.
- TODO: sBOA integration.
- Adjust normalization of value computed by FourPeaks and SixPeaks fitness functions, must be between [0,100].
- Add to sBOA unsupported objective problem (SatLib, SpinGlass, TextureRestoration).
- TODO DEUM: svd resolutor causes problems durign execution.
- TODO export data in tgz not in tar