Template based paper like reconstruction when the edges are straight
Contents
Project profile
Aim of this project is to reconstruct the deformation of a paper given the images of the paper itself and of the picture on the page. The assumption made is that the paper edges are straight.
A related work is Template-Based Paper Reconstruction from a Single Image is Well Posed when the Rullings are Parallel,
P. Taddei and A. Bartoli NORDIA'08 - Workshop on Non-Rigid Shape Analysis and Deformation Image Alignment at CVPR'08, Anchorage, Alaska, June 2008 (the presentation of this work is available here in pdf)
Dates
Start date: 2008/06/02
End date: 2008/12/31
People involved
Project head(s)
- Pierluigi Taddei
- Vincenzo Caglioti
Students currently working on the project
Laboratory work and risk analysis
This project does not include laboratory activities.
Project description
The problem
Aim of the project is is the implementation of an error function whose minimization allows the reconstruction of a deformed paper like surface.
While the problem is ill-posed in the general case, it is possible to demonstrate that the reconstruction problem can be simplified considering those isometries that map the template to a developable surface wih two opposite straight edges.
To solve this problem the image template (2D image in real dimension of the paper), the perspective image (the 2D image of the deformed paper), a set of points correspondences between the two images and the camera calibration matrix are given.
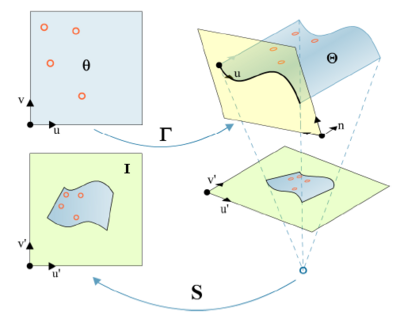
Under these constraints, the problem can be formulated as shown in the following pictures:
Image <math>\theta</math> is the template image, which represents the projection on the 2D space of the same paper in the 3D space, represented by image <math>\Theta</math>. <math>\Gamma</math> is the function that transforms each point of <math>\theta</math> into a point of <math>\Theta</math>. <math>\Gamma</math> is the unknown matrix that will be iteratively modified in order to minimize an error function. S is the camera calibration matrix that maps the 3D object <math>\Theta</math> into the image I. The known points’ correspondences are the one on <math>\theta</math> and I images, while points on <math>\Theta</math> are unknown.
The error terms
The implemented error function takes into account several error terms:
- reprojection error: this is the error between the known points on I image and the projection on I of the known points on <math>\theta</math>
- smoothness error: in the construction of <math>\Theta</math> the edges not constrained to remain parallel must be the smoothest as possible
- lower edge length preservation: in the construction of <math>\Theta</math> the lower deformable edge must maintain the same length of the same edge on <math>\theta</math>
- upper edge length preservation: in the construction of <math>\Theta</math> the upper deformable edge must maintain the same length of the same edge on <math>\theta</math>
- height preservation: in the construction of <math>\Theta</math> the paper height (the length of the non deformable edges) must be maintained on the entire surface
The error terms forms the error array: to improve the following minimization, the Jacobian matrix of the array has been calculated too.
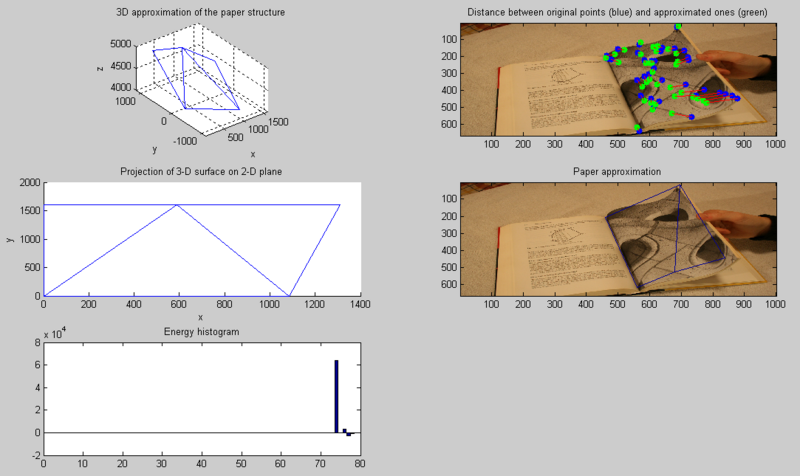
The function calculating the error and a testing environment for the function has been implemented in Matlab; several information about the solution can be shown:
- a 3D graphs of <math>\Gamma</math> function
- the projection on the 2D space of <math>\Gamma</math> function
- a histogram whose bar represents the error terms
- the I image with the distance between the a priori known points on I image and the projection on I of the a priori known points on <math>\theta</math>
- the I image with the approximation of the paper given by the projection on <math>\Gamma</math> on I
An example of the displayed information is shown in the following picture:
Documentation
The documentation about the project is available here: Documentation.
It contains the explanation about the calculated error and, since the code (for performance reason) has been written in a non intuitive way, the detailed documentation of the Matlab code.
Conclusion
This project puts the basis for paper reconstruction with the implementation of an error function whose minimization improves the approximation in the 3D space of the paper surface.
Future works will involve the search of an initial vector for the minimization and the study of the relative importance the single error terms have, formulating feasible error weights per which the error terms will be multiplied.